Math B
Area and Perimeter of Triangles, Parallelograms, and Rhombuses
A triangle is a polygon with three sides and three angles. A parallelogram is a quadrilateral with two sets of parallel sides, the opposite sides being of equal length and the opposite angles congruent. A rhombus is a four-sided polygon where every side has the same length. A rhombus can also be defined as an equilateral quadrilateral. Area is the amount of space, or the two-dimensional size, taken by a figure or object. Perimeter is the distance around a shape, or figure.
Triangles
To find the area of a triangle, you must multiply the base by the height and then the quotient by a half.
For an acute triangle, the base can be any side of the triangle. The height is a line drawn from the base to the opposite point, or corner, of the base. An equation you can use can be Area = 1/2bh . The variable would represent the base and the variable would represent the height.
For a right triangle, the height is the line opposite of the hypotenuse.
For an obtuse angle, dotted lines are drawn to make it look like a right triangle. However, only the line opposite of the hypotenuse is used. This line is used to find the height. The base’s measurement remains the same.
examples:
1.
2.
3.
To find the perimeter of a triangle, you simply have to add up the length of each side together. A formula you could use to find the perimeter of a triangle could be Perimeter = a+b+c , where each variable represents a different side of the triangle.
example:
Parallelograms
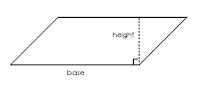
To find the area of a parallelogram, you must multiply the base by the height. The base can be any side of the parallelogram and the height is found by drawing a dotted line.
The formula for finding the area of a parallelogram is A = b x h. b being the base and h being the height.
example:
To find the perimeter of a parallelogram, all you have to do is add up the length of its sides. A parallelogram has two sets of parallel sides. Knowing this, you could use the formula Perimeter = 2a + 2b . The variable a would represent the length of one of its shorter sides, and b would represent the length of one of its longer sides.
example:
Rhombi
To find the area of a rhombus, you must first multiply the lengths of the diagonals. Then you must divide the product by two. A diagonal is a line drawn from one point, or corner, to the point opposite of it.
A formula you could use to find the area of a rhombus is 1/2xy. The variable would represent the length of one diagonal and the variable would represent the length of the other diagonal.
example:
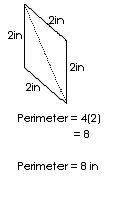
Each side of a rhombus is equal. To find the perimeter of a rhombus, adding each side is optional. But to make it easier, you can multiply the length of one side, since it is the same as the others, by four.
example:
Practice Problems
Find the area of the following
1.
2.
3.
4.
5.
Find the perimeter of the following
6.
7.
8.
No comments:
Post a Comment